

What is packing efficiency calculate packing efficiency of BCC?Ī BCC unit cell has 2 atoms per unit cell. Packing efficiency is always calculated in percentage. APF for the simple cubic structure 0.52 ATOMIC PACKING FACTOR (APF) contains 8 x 1/8 1atom/unit cell Lattice constant close-packed directions a R0.5a. For a simple cubic lattice, the packing efficiency is 52.4 and the. In atomic systems, by convention, the APF is determined by assuming that. The packing efficiency of both of these is 74 which means 74 of the space is filled. It is dimensionless and always less than unity.
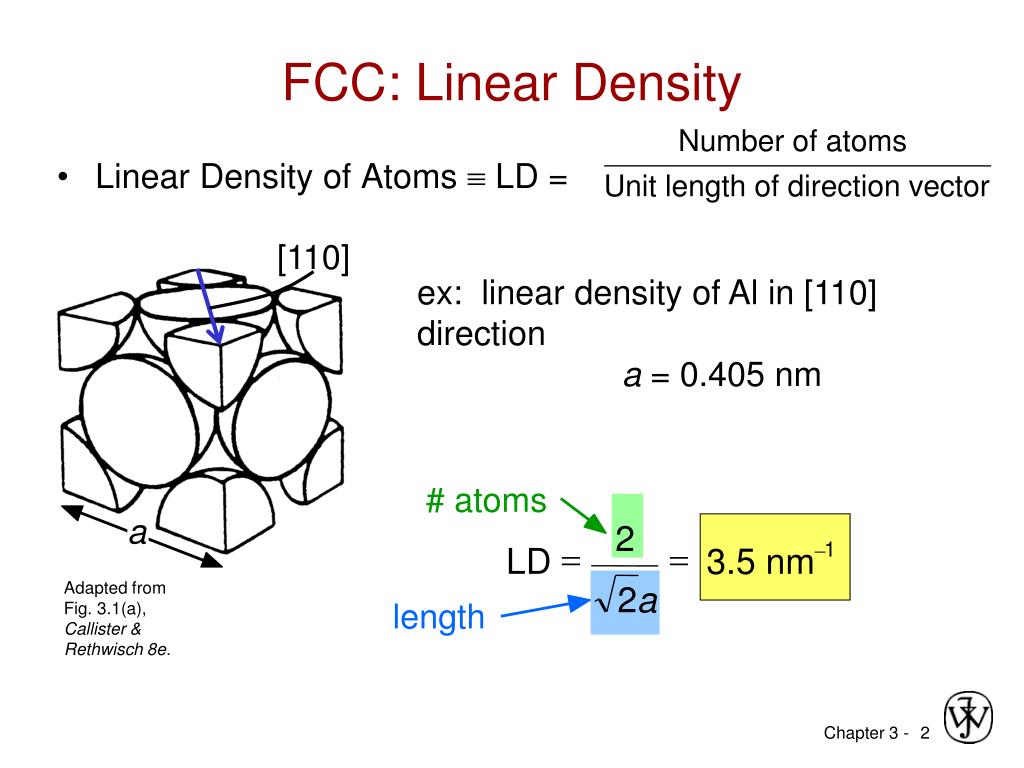
In crystallography, atomic packing factor (APF), packing efficiency or packing fraction is the fraction of volume in a crystal structure that is occupied by constituent particles. Mathematically it is the volume occupied by atoms in a unit cell divided by the total volume of the unit cell, the whole multiplied by 100. Atomic Packing factor for SC BCC FCC and HCP. With the help of packing efficiency, the quantitative aspect of solid state can be done. How do you calculate packing efficiency of BCC? Atomic packing factor - In crystallography, atomic packing factor (APF) or packing fraction is the fraction of volume in a crystal structure that is. … The unit cell of BCC has spheres in the corners of a cube and one sphere in the centre of the cube. BCC stands for body-centred cubic structure whereas FCC stands for face-centred cubic structure. By viewing atoms as hard spheres it is straightforward to calculate the packing fraction for common crystal structures such as the simple cubic (0.524), the.

The terms BCC and FCC are used to name two different arrangements of crystalline structures. Also, for FCC a = 2√2 r where a is the side of the cube and r is the atomic radius. How do you find the atomic packing factor of the FCC? What is the atomic packing factor of bcc structure Mcq?Ītomic packing factor of body centred cubic structure (bcc) is 0.68. Thus 32 % volume is empty space (void space). The packing efficiency of the body-centred cubic cell is 68 %. What is the packing fraction of bcc unit cell? Body-centered cubic (bcc): 0.68.What is the atomic packing factor of bcc and fcc respectively? The packing density in the hcp-lattice thus also has the maximum possible value of 74 %.The packing factors of slip systems include: Hexagonal close-packed (hcp): 0.74. However, there is no need to differentiate between the fcc-structure and the hexagonal closest packed crystal (hcp), since in both cases they built up by densest packed atomic planes (for further information see post on Important lattice types). Because the volume of the corner atoms are.
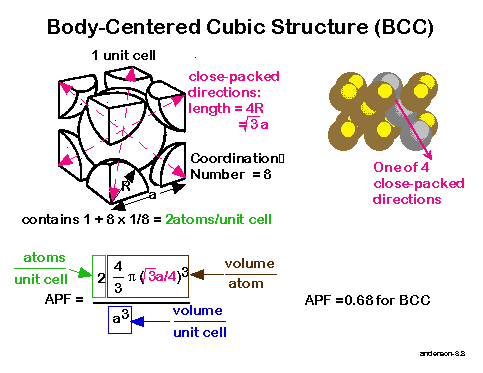
The fcc-lattice thus has an packing factor of 74 %. The body-centered cubic crystal structure contains eight atoms on each corner of the cube and one atom in the center. The packing density is the ratio of atomic volume \(V_A\) within a unit cell to the total volume of the unit cell \(V_ BCC has 2 atoms per unit cell lattice constant a 4R3 Coordination number CN 8 and Atomic Packing Factor APF 68. The packing factor of BCC is 0.68: The packing factor of FCC is 0.74: Number of Spheres in a Unit Cell: A unit cell of BCC has a net total of 2 spheres. Notes: Characteristics of various types of structures are shown in the table below: Characteristics. A P F N a t o m s V a t o m V c r y s t a l 4 ( 4 3) r 3 ( a) 3 4 ( 4 3) r 3 ( 2 2 r) 3. Of course there are still low-melting point metals with FCC HCP or BCC crystal structures because these are the most stable structures. Also, for FCC a 22 r where a is the side of the cube and r is the atomic radius. 3 Face-centered cubic and hexagonal closest packed lattice (fcc, hcp) Atomic Packing Factor The ratio of atomic sphere volume to unit cell volume assuming a hard sphere model.


 0 kommentar(er)
0 kommentar(er)
